Studium Grafische Faltung

[MAGIo]

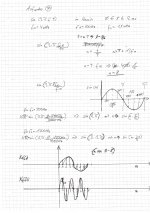
Hallo, es ist ein simpler Einstieg in die grafische Faltung, jedoch krieg ich es mit meinen Mitschriften (doch sehr lueckenhaft) nicht rekonstruiert, was dort gemacht wurde.

Es handelt sich um folgende Aufgabe

Ein Signal x(t) = rect(t -1/ 2)wird an den Eingang eines Übertragungssystems gelegt, dessen
Stossantwort ebenfalls h1(t) = rect(t -1/ 2) ist.
a) Bestimmen und skizzieren Sie das Ausgangssignal y(t).

Das Signal y(t) wird auf ein weiteres System mit der Stossantwort
h2(t) = rect(t - 1/2) gegeben.
b) Bestimmen und skizzieren Sie auch dieses Ausgangssignal.


Ich verstehe es aber irgendwie vorne und hinten nicht, denke das duerfte fuer Euch kein Problem darstellen. THX

 

[sklemm]

Man könnte dir eher helfen, wenn man wüsste wo genau dein Problem liegt, ich versuche es mal kurz:

Der Übersichtlichkeit halber wird der Zeitparameter beider Funktionen in τ umbenannt, also aus x(t) wird x(τ) und aus h1(t) wird h1(τ).
Als nächstes spiegelst du eine der beiden Funktionen an der vertikalen Achse, sagen wir mal x(τ) -> x(-τ)
Um jetzt den Wert y(t) zu bestimmen verschieben wir x(τ) um t (deshalb die Umbenennung des Zeitparameters.
Jetzt werden beide Funktionen miteinander Multipliziert.
Zum Abschluss integriert man von -∞ bis +∞.

Was sollte grafisch rauskommen:
Mit wachsendem t nähert sich von links ein Rechteck dem anderen(vorher wurde schon gespiegelt). Durch die Multiplikation bleibt alles null bis sich die beiden beginnen zu überlappen. Mit der Überlappung ergibt sich eine neue Rechteckfunktion mit der Breite der Überlappung. Die Integration liefert anschließend den Flächeninhalt des Rechtecks. Dieser Wert ist der Wert der Ausgangsfunktion an der Stelle t.

Ich hoffe das hat geholfen, wenn nicht sag mal wo du aussteigst, dann kann man es vielleicht an der Stelle noch etwas vertiefen. Ansonsten kann es vielleicht helfen sich vorzustellen was das Faltungsintegral an sich macht. Alle Schritte der grafischen Lösung finden sich ja darin auch.

HTH

 

[theHacker]

Ein ähnlicher Thread, in dem die grafische Faltung erklärt wird:
https://www.klamm.de/forum/showthread.php?t=193848

 

[MAGIo]

Ich habe jedoch ein Problem mit der Unterteilung in verschiedene Fälle. In meiner Musterlösung habe ich 2 Fälle, die ich weder richtig entziffern, noch nachvollziehen kann!

Wie gesagt, eigentlich ist das nur der Einstieg in diese Art von Aufgaben... Aber da hakt es schon!

 

[DaPhreak]

Ich habe jedoch ein Problem mit der Unterteilung in verschiedene Fälle. In meiner Musterlösung habe ich 2 Fälle, die ich weder richtig entziffern, noch nachvollziehen kann!

Teilaufgabe a) oder b)? Wenn a), hast Du Dir mal die Erklärung von mir in dem anderen Thread angeschaut? Bist Du da mitgekommen und wenn nein an welcher Stelle genau nicht mehr?

Wir haben Deine Musterlösung nicht also können wir kaum erraten was für zwei Fälle das sein sollten. Ich kann nur raten, dass es sich dabei um die steigende und die fallende Flanke des resultierenden Dreiecks handelt. Aber das bringt uns nicht weiter. Versuch doch erstmal selbst die Erklärung von mir nachzuvollziehen, dann verstehst Du vielleicht auch Deine Musterlösung besser.

 

[MAGIo]

Hi, ich bin seit zirka 24 Stunden schon an Deiner Musterlösung in groß ausgedruckten Seiten dran. Mittlerweile ist gar nichts mehr erkennbar, wegen meinen eigenen Notizen. Es ist echt unglaublich, wie man etwas vermeintlich einfaches kompliziert machen kann

Also...

Meine erste Problematik ist schon das Auftreten von t und T(Tau), wobei ich ja nachvollziehen kann, dass T eine Verschiebevariable ist. Doch in dem Ergebnis, zeichne ich dann den Graphen in Abhängigkeit von t oder T?

Mein Hauptproblem ist jedoch, weshalb ist in der graphischen Lösung plötzlich h(t-T), dies würde doch rein logisch bedeuten, dass die Funktion von t nach rechts um T verschoben wird. Auch alles logisch, IN MEINEM KOPF.. aber nicht auf Papier

Und das allergrößte Problem ist die Realisation per Rechenweg, damit alles auch nachvollziehbar und ausführlich dort steht. In meinem Beispiel habe ich die Lösung im Bereich 0 <=t <=1 (was ich schon nicht verstehe) mit einem Integral 1 * 1 dT von 0 bis t, welches t ergibt.
Im zweiten Teil ein Integral von (t-1) bis 1, welches 2-t ergibt.

Am liebsten würd ich das scannen, da ich denke es ist zu unverständlich. Doch bin ich nicht zu Hause und habe keinen Scanner parat. Hoffe es ist trotzdem noch irgndwie verständlich. Ich denke es ist eine bestimmte Stelle, die ich selber nicht erkenne. Wie eine Blockade...

 

[DaPhreak]

Meine erste Problematik ist schon das Auftreten von t und T(Tau), wobei ich ja nachvollziehen kann, dass T eine Verschiebevariable ist. Doch in dem Ergebnis, zeichne ich dann den Graphen in Abhängigkeit von t oder T?

Man zeichnet natürlich in Abhängigkeit der Verschiebevariablen, in meiner Erklärung wäre das t. Das ist doch die Idee: zeichne die gemeinsame Fläche der beiden Funktionen wenn man sie t gegeneinander verschiebt. Also hängt das Ergebnis nur noch von t ab.

Das τ wird halt rausintegriert:

∫-∞ bis +∞ h1(τ)h1(t-τ) dτ

zumindest definiere ich es sorum. Was man t und was τ nennt ist Geschmackssache. Verschiebezeit = τ wäre vielleicht logischer gewesen, aber ich will jetzt nicht den ganzen Post umbauen.

Mein Hauptproblem ist jedoch, weshalb ist in der graphischen Lösung plötzlich h(t-T), dies würde doch rein logisch bedeuten, dass die Funktion von t nach rechts um T verschoben wird. Auch alles logisch, IN MEINEM KOPF.. aber nicht auf Papier

Wenn es logisch in Deinem Kopf ist musst Du es doch nur noch aus Deinem Kopf auf's Papier bringen...

Und das allergrößte Problem ist die Realisation per Rechenweg, damit alles auch nachvollziehbar und ausführlich dort steht. In meinem Beispiel habe ich die Lösung im Bereich 0 <=t <=1 (was ich schon nicht verstehe) mit einem Integral 1 * 1 dT von 0 bis t, welches t ergibt.
Im zweiten Teil ein Integral von (t-1) bis 1, welches 2-t ergibt.

Ist grade für Rechtecke sehr unüblich, das auf dem Rechenweg zu lösen, aber kann man natürlich machen.

Bei Dir ist ja nur anders, dass Deine Rechtecke beide kausal sind, also von 0 bis 1 gehen. Damit hast Du das gespiegelte von -1 bis 0. Eine Überlappung gibt es folglich nur für positive Verschiebungen t. Dazu zwei Fälle, einmal von 0 bis 1, da wächst die gemeinsame Fläche linear von 0 auf 1 an, das Integral gibt also t. Dann von 1 bis 2, da fällt die Überlappung linear ab, beginnt aber für t=1 bei 1. Deshalb 2-t: das ist 1 für t=1 und 0 für t=2, so wie es sein muss.


Ich verstehe leider wirklich nicht, an welcher Stelle Du nicht mitkommst. Vielleicht kannst Du das noch präzisieren.

 

[sklemm]

Meine erste Problematik ist schon das Auftreten von t und T(Tau), wobei ich ja nachvollziehen kann, dass T eine Verschiebevariable ist. Doch in dem Ergebnis, zeichne ich dann den Graphen in Abhängigkeit von t oder T?

Wenn ich das im anderen Posting richtig sehe, musst du darauf achten, dass die Beschreibung der grafischen Lösung nicht ganz konsistent mit den Gleichungen ist. In der grafischen Lösung wird um τ verschoben, im Integral um t.
Ich hangel mich jetzt an den Bezeichnungen der Gleichungen weiter.
Die Integrationsvariable ist τ, d.h. nach dem Integrieren ist das τ weg und es steht nur noch t da. t ist dann auch die Verschiebung der beiden Funktionen zueinander. Das ergibt auch Sinn, wenn du dir die Kommentare am Ende von daPhreaks Posting ansiehst und die Rechnung da als Autokorrelationsfunktion erkennst. Musst du aber vorerst auch nicht.

Mein Hauptproblem ist jedoch, weshalb ist in der graphischen Lösung plötzlich h(t-T), dies würde doch rein logisch bedeuten, dass die Funktion von t nach rechts um T verschoben wird. Auch alles logisch, IN MEINEM KOPF.. aber nicht auf Papier

Also h(t) ist die Ausgangsfunktion, der Parameter wurde umbenannt in h(τ) und gespiegelt h(-τ). Und jetzt um t nach rechts verschoben h(t-τ).

Und das allergrößte Problem ist die Realisation per Rechenweg, damit alles auch nachvollziehbar und ausführlich dort steht. In meinem Beispiel habe ich die Lösung im Bereich 0 <=t <=1 (was ich schon nicht verstehe) mit einem Integral 1 * 1 dT von 0 bis t, welches t ergibt.
Im zweiten Teil ein Integral von (t-1) bis 1, welches 2-t ergibt.

OK, nach dem Spiegeln hast du für t=0 zwei Rechtecke, eines links der Achse und eins rechts, beide mit breite 1 und höhe 1.
Das Produkt beider Fkt'en ist konstant 0. Soweit klar?
Jetzt setzen wir t auf z.B. 0,1. das linke Rechteck wandert um 0,1 nach rechts, dadurch wird das Produkt beider Fkt'en im Bereich von 0 bis 0,1 = 1, sonst wieder 0. Das Integral liefert dir 0,1. Das ist auch y(t=0,1). Für t=0,5 solltest du dann auf y(t=0,5)=0,5 kommen.
Jetzt setzen wir t=1, damit überlappen sich beide Rechtecke komplett und y(t=1) = 1.
Das war höchstwahrscheinlich der erste Fall deiner unleserlichen Fallunterscheidung

Wenn du das jetzt richtig rechnen willst, musst du den Integrationsbereich in 3 Teile teilen, einmal von -∞ bis 0, da liefert es 0, weil x(τ) h(t-τ) = 0.
Der zweite Teil ist von 0 bis t, der liefert t, weil x(τ) h(t-τ) = 1.
Im dritten Teil von t bis +∞ ist wieder x(τ) h(t-τ) = 0 und das Integral liefert 0.
Diese Fallunterscheidung musst du machen, weil das Riemann-Integral stetige Funktionen mag, was die Rechteckfunktion ja nicht ist.

HTH

Edith meint: Oh, dar war Phreak schneller, aber ich lasse es jetzt auch mal stehen, vielleicht hilft doppelt ja besser :-D

 

[MAGIo]

Also ich glaube meine Problematik setzt sich nun schon seit zig Stunden daraufhin fest, dass ich mich zu sehr an schematischem Vorgehen orientiere. Ist ja gerade in so einer Sache auch nicht verkehrt, trotzdem habe ich verschiedene Lösungen und daher ist das Durcheinander nicht verwunderlich.

Nun denke ich, dass ich beim rechnerischen Weg die Intervalle bzw. Fallunterscheidungen nicht richtig interpretieren bzw. finden kann, so habe ich im Skript eine recht komplexe Lösung (RC Glied, also keine lineare Funktion) mit klar definierten Intervallen (zB 0 bis 2) beim Integral, jedoch bei der besprochenen Aufgabe dann zB von 0 bis (t-2) oder Ähnlich.

Hoffe Ihr versteht meine Problematik langsam, es ist schrecklich wenn es im Kopf irgendwie einen Sinn macht, aber es nicht auf Papier zu bringen ist. Genauso kann ich nicht konkret sagen wo das Problem ist, aber faktisch ist ein Problem vorhanden!

 

[DaPhreak]

Nun denke ich, dass ich beim rechnerischen Weg die Intervalle bzw. Fallunterscheidungen nicht richtig interpretieren bzw. finden kann, so habe ich im Skript eine recht komplexe Lösung (RC Glied, also keine lineare Funktion) mit klar definierten Intervallen (zB 0 bis 2) beim Integral, jedoch bei der besprochenen Aufgabe dann zB von 0 bis (t-2) oder Ähnlich

Deshalb sage ich ja: Gerade Faltungen von Rechtecken mit Integration zu lösen ist ziemlich nervig, würde ich meinen Studenten nie abverlangen. Das Problem hierbei sind einfach die stückweise definierten Funktionen die zu sackweise Fallunterscheidungen führen und das macht nicht viel Spaß. Ich empfehle meinen Studenten im Seminar deshalb immer gerade sowas wie Rechtecke lieber grafisch zu falten, da kommt man viel schneller zu einer Lösung und hat weniger Dinge die schief gehen können.

Oder natürlich man berechnet gleich die Fouriertransformierten und multipliziert dann im Bildbereich ganz einfach.

 

[MAGIo]

Naja,es ist nunmal Aufgabenstellung und ich muss das auch noch heute verstehen. Aber da faellt mir ein anderes Problem auf, welches vll. erstmal einfacher zu loesen ist.

Ich fuege einfach den Aufgabentext ein, ist einfacher.

Ein Sinussignal sin(2 ×p × f × t) wird im Bereich 0 £ t £ 2 ms mit einer Abtastfrequenz von 4 kHz
abgetastet, wobei die Abtastung bei t=0ms beginnt.
a) Bestimmen und skizzieren Sie die Abtastwerte für f1=500Hz und f2=1500 Hz.
____________________________________________________________

b) Die Abtastwerte werden auf das Übertragungssystem mit der Impulsantwort h(-1) = h(1) = -0.25
und h(0) = 0.5 und h = 0 für n<-1 und n>1 gegeben. Bestimmen und skizzieren Sie die
Abtastwerte der Ausgangssignale.

a) ist stellt kein Problem dar. b) sollte eigentlich auch keines sein, doch trotzdem komme ich immer auf ein falsches Ergebnis.
Ich benutze um es rechnerisch zu loesen die Formel
Y= SUMME x(m) * h (n-m)

Bisschen schwierig hingeschrieben, aber verstaendlich. Was ist mein m? Rein logisch wuerde ich sagen, die 8 Werte aus Aufgabenteil a, also m geht von 0 bis 8. Nur scheint sich das mit der Loesung nicht zu decken...

 

[DaPhreak]

Ich benutze um es rechnerisch zu loesen die Formel
Y= SUMME x(m) * h (n-m)

Bisschen schwierig hingeschrieben, aber verstaendlich. Was ist mein m? Rein logisch wuerde ich sagen, die 8 Werte aus Aufgabenteil a, also m geht von 0 bis 8. Nur scheint sich das mit der Loesung nicht zu decken...

Das m geht von -? bis +?, immer. Natürlich ist dein x(m) = 0 für alle m<0 und m>8. Selbes gilt für h(m). Damit kannst Du alle Terme weglassen, wo entweder x(m) schon null ist oder h(n-m).

Damit ergeben sich die Grenzen:
aus x(m): m?8 und m?0
aus h(n-m): n-m?-1 => m?n+1 und n-m?1 => m?n-1

Zusammen: max(0,n-1) ? m ? min(8,n+1)

D.h.
für alle 1?n?7 sind die Grenzen n-1?m?n+1
für alle -1?n<1 geht es von 0 bis n+1
für alle n<-1 gibt es gar keine Terme (kommt 0 raus).
für alle 7<n?9 geht es von n-1 bis 8
für alle n>9 gibt es auch keine Terme (wieder 0).

*edit*
Hier gibt's ne ganz nette Java-Demo dazu: Joy of Convolution.

*edit2*
Schneller und übersichtlicher geht das ganze mit der Matrix/Vektorschreibweise der diskreten Faltung aber das habt ihr bestimmt nicht behandelt.

*edit3*

Hab doch noch mal 'ne Tabelle erstellt, da ist es etwas übersichtlicher: In den Zeilen n, in den Spalten m, dort drin jeweils die Terme eingetragen, die nicht Null sind. Um ein y[n] zu bekommen musst Du jetzt jeweils eine Zeile durchgehen und entlang der Zeile alle Terme aufsummieren. Da siehst Du ganz gut wie die Grenzen für m sich entwickeln, erst {0}, dann {0,1}, {0,1,2}, {1,2,3}, {2,3,4}, usw. bis {6,7,8}, {7,8}, {8}.

Hier ist das Meisterstück:

 

[MAGIo]

Seh ich genauso, doch leider habe ich eine Loesung, die genau was Anderes wiedergibt. Hier die Scans, das erleichtert vll Einiges. Wenn das erledigt ist, setze ich noch mein Problem bei der urspruenglichen Aufgabenstellung rein, da sagen Bilder wohl mehr als Worte... zumindest ungluecklich gewaehlte

 

[DaPhreak]

Seh ich genauso, doch leider habe ich eine Loesung, die genau was Anderes wiedergibt.

Was genau ist da jetzt anders?

Okay, noch paar mehr Terme weggelassen, weil beispielsweise x[0] und x[8] zwar schon in dem Intervall [0,2ms] liegen aber eben als Abtastwert trotzdem genau eine null liefern. Ist doch aber egal,in der Rechnung sollte das gleiche rauskommen.

 

[MAGIo]

ja leider ist schon beim ersten Wert keine Null, also fuer Y(0)...

und in der Musterloesung kommen allgemein recht andere Werte raus. Ich war einfach schon in der Sache so verunsichert, dass ich auch gar nicht mehr an mein Koennen glaube. Das ist schon traurig, daher hatte ich auch den Antrieb nicht mehr das zu Ende zu rechnen, weil ich ganz genau weiss, dass das falsch sein MUSS...

 

[DaPhreak]

Sorry aber ich kann echt kaum was entziffern, weder bei Deinem Gekrakel noch bei der "Musterlösung". Sag denen mal die sollen die in LaTeX setzen das ist ja ne Katastrophe. Und schreib Deine sauber auf, dann kann ich Dir sagen was falsch ist.

MATLAB kommt, wenn ich mich nicht vertippt habe, für Signal 1 (500 Hz) auf die folgenden Abtastwerte für y, n=0, 1, ..., 8:

[-0.1768 0.1036 0.1464 0.1036 0.0000 -0.1036 -0.1464 -0.1036 0.1768]

*edit* Hier zur Kontrolle nochmal ein Plot:

 

[MAGIo]

was hast Du in MATLAB dafuer eingegeben als Syntax, dann versuche ich es auch einmal...

 

[MAGIo]

Danke, Du bist meine Rettung. Jetzt nur noch das urspruengl. Problem, danke das Du mir dann doch wieder etwas Vertrauen in mein Koennen gegeben hast. Ist schwierig, wenn man sonst kaum Resonanz kriegt und dann auch recht schnell gefrustet ist...

So, hier mein Ansatz zur urspruenglichen Aufgabe. Den grafischen Teil habe ich nun erstmal weggelassen, Fokus auf das Rechnerische. Leider verstehe ich es nicht, wieso und weshalb diese Grenzen gewaehlt wurden und die Intervalle.

 

[DaPhreak]

was hast Du in MATLAB dafuer eingegeben als Syntax, dann versuche ich es auch einmal...

fp = 4000;t0 = 1/fp;
taxis  = 0:t0:2e-3;
sig1 = sin(2*pi*taxis*500)
h = [-0.25,0.5,-0.25];
y = conv(h,sig1);

So, hier mein Ansatz zur urspruenglichen Aufgabe. Den grafischen Teil habe ich nun erstmal weggelassen, Fokus auf das Rechnerische. Leider verstehe ich es nicht, wieso und weshalb diese Grenzen gewaehlt wurden und die Intervalle.

Naja, Rechteck 1 geht von 0 bis 1, Rechteck 2 gespiegelt von -1 bis 0 und wird dann allmählich reingeschoben:

Fall 1: Rechteck kommt von rechts rein, die Überlappung wächst immer weiter an, es überlappt sich von 0 bis t, deshalb die Integrationsgrenzen.

Fall 2: Rechtecke überlagern sich erst ganz (von 0 bis 1), dann wird Rechteck 2 langsam nach rechts rausgeschoben. Deshalb bleibt die obere Grenze auf 1, die unter steigt aber von 0 auf 1 an, deshalb t-1.

 

[MAGIo]

klingt einfacher als es ist.Ich kann die Grenzen zB schematisch nicht erkennen... haette jetzt von 0 bis 1 bzw. 1 bis 2....